Generation of optical Schrödinger “cat” states in intense laser-matter interactions
In a theoretical and experimental study published in Nature Physics, an international team of researchers (from ICFO/ICREA-Spain, Technion-China, MBI-Germany, ELI-ALPS-Hungary, UoC and FORTH-Greece) led by Prof. Maciej Lewenstein (ICFO-Spain) and Dr. Paraskevas Tzallas (Research Director at FORTH and academic visitor of the Physics department of the UoC), demonstrates the generation of highly non-classical states of light in intense laser–atom interactions. The theory has been developed by J. Rivera-Dean (ICFO), M. F. Ciappina (Technion-China), E. Pisanty (MBI-Germany), P. Stammer (ICFO) and M. Lewenstein, and the experiment has been performed at FORTH-IESL by Th. Lamprou (PhD student in the Department of Physics of the University of Crete) and P. Tzallas, Researcher at IESL/FORTH and Academic Visitor at the Dept. of Physics of the Univ. of Crete.
Over the past four decades, astounding advances have been made in the field of laser technologies and the understanding of light-matter interactions in the non-linear regime. Thanks to this, scientists have been able to carry out extremely complex experiments, using ultra-fast light-pulses in the visible and infrared range, to accomplish crucial milestones such as using a molecule’s own electrons to image its structure, to see how it rearranges and vibrates or breaks apart during a chemical reaction.
The development of high-power lasers allowed scientists to study the physics of ultra-intense laser–matter interactions which, in its standard version, treats ultra-strong ultra-short driving laser pulses only from a classical point of view. The famous theory coined as the “simple man’s model” or the “three-step model” – which had its 25th anniversary in 2019 – dealt with the interaction of an electron with its parent nucleus sitting in a strong laser field environment, and elegantly described it according to classical and quantum processes. However, due to the fact that these laser pulses are highly coherent and contain huge numbers of photons, the description of the interaction in the strong field has so far been incomplete, because it treated the atomic system quantum mechanically, but the electromagnetic field classically.
Now, in the description of the most important processes of ultra-intense laser–matter physics (such as high-harmonic generation (HHG), above threshold ionization, laser-induced electron diffraction, sequential and non-sequential multi-electron ionization, etc.) the quantum-fluctuation effects of the laser electric or magnetic fields are negligible. However, the quantum nature of the entire electromagnetic fields is always present in these processes, so a natural question arises: does this quantum nature exhibit itself? In which situations does it appear?
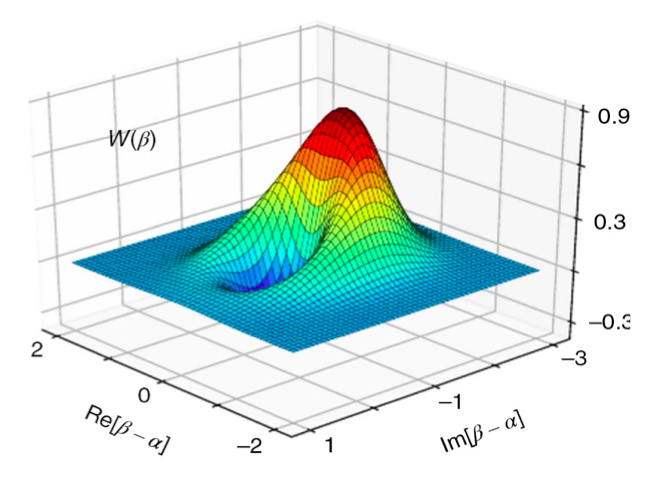
In the recent study published in Nature Physics, the authors have demonstrated that intense laser–atom interactions can lead to the generation of highly non-classical states of light. Such results have been obtained by using the process of HHG in atoms, in which large numbers of photons, from an infrared driving-laser pulse, are up-converted into photons of higher frequencies in the extreme ultraviolet spectral range. The quantum electrodynamical theory, formulated in this study, predicts that if the initial state of the driving laser is coherent, it remains coherent, but shifted in amplitude after interactions with the atomic medium.
Similarly, the quantum states of the harmonic modes become coherent with small coherent amplitudes. However, the quantum state of the laser pulse that drives the HHG can be conditioned to account for this interaction, which transforms it into a so-called optical Schrödinger cat state. This state corresponds to a quantum superposition of two distinct coherent states of light: the initial state of the laser, and the coherent state reduced in amplitude that results from the interaction with the atoms.
The researchers accessed the full quantum state of this laser pulse experimentally using quantum state tomography. To achieve this, the coherent amplitude of the light first needs to be reduced in a coherent way to only a few photons, on average, and then all of the quantum properties of the state can be measured.
The results of this study open the path for investigations towards the control of the non-classical states of ultra-intense light, and exploiting conditioning approaches on physical processes relevant to HHG. This hopefully will link ultra-intense laser-matter physics and atto-science to quantum information science and quantum technologies in a novel, and completely unexpected manner.
Research Article: “Generation of optical Schrödinger “cat” states in intense laser-matter interactions” by M. Lewenstein, M. F. Ciappina, E. Pisanty, J. Rivera-Dean, P. Stammer, Th. Lamprou and P. Tzallas, Nature Physics (2021).




