Evanescent-wave chiral optical rotation measurements by signal-reversing cavity-based polarimetry
The optical measurement of chirality is of fundamental importance to many fields, with applications ranging from drug design and synthesis, the determination of protein structure, to the measurement of atomic parity violation as a low-energy test of the Standard Model. The most widely used optical techniques are the traditional methods of circular dichroism (CD) and optical rotatary dispersion (ORD). However, these chiral signals are typically very weak (of order 10-6 compared to the achiral signals), and their measurement is limited by larger time-dependent backgrounds (such as spurious birefringence) and by imperfect and slow subtraction procedures.
The group of Professor Peter Rakitzis, at the University of Crete & the Foundation for Research and Techology-Hellas (FORTH), has demonstrated a bowtie-cavity-based polarimeter with counter-propagating beams, which solves these problems: the chiral signals are enhanced by the number of cavity passes (typically>103); the effects of linear birefringence are suppressed by a large induced intracavity Faraday rotation; and rapid signal reversals are effected by reversing the Faraday rotation and subtracting signals from the counter-propagating beams. The signal reversals, in particular, allow the absolute measurement chirality without needing to remove the sample, which is the major drawback of all other polarimeters. These advantages allow measurements of absolute chiral signals in environments where background subtractions are not feasible, and conventional polarimeters fail. For the first time, chiral ORD was measured in the evanescent wave produced by total internal reflection at a prism surface, from (+)-maltodextrin and (-)-fructose solutions. These measurements confirm the Drude-Condon model for Maxwell’s equations in isotropic optically active media. In particular, the effective ORD path length, near index matching, is shown to be equal to the Goos-Hänchen shift (GHS) of the evanescent wave. The limits of this polarimeter, when using a continuous-wave laser locked to a stable high-finesse cavity, should match sensitivity measurements for linear birefringence (3x10-13 rad), which is several orders of magnitude more sensitive than current chiral detection limits, transforming the power of chiral measurements in many fields
Reference: "Evanescent-wave and ambient chiral sensing by signal-reversing cavity-ringdown polarimetry” by Dimitris Sofikitis, Lykourgos Bougas, Georgios E. Katsoprinakis, Alexandros K. Spiliotis, Benoit Loppinet and T. Peter Rakitzis, Nature 514, 76-79 (2 October 2014).
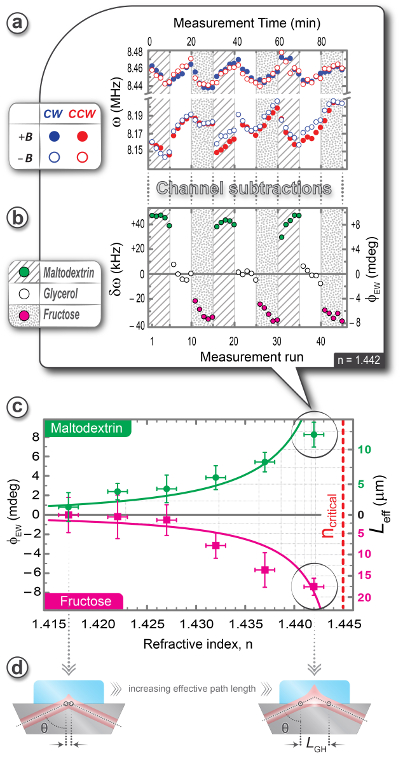
Figure: a, The four polarization rotation frequencies ![]() ,
, ![]() ,
, ![]() and
and ![]() and , are shown for evanescent-wave measurements of maltodextrin, glycerol (a non-chiral reference sample with zero optical rotation), and fructose solutions, all with refractive index n=1.442. The solutions are changed with a flow cell every 10 minutes. b, Subtractions of the polarization frequencies isolate the optical rotation of the samples in the evanescent wave, out of larger achiral backgrounds. c, Measurements for solutions with n=1.417-1.442. Error bars are 2σ confidence intervals. The theoretical curves are generated using the Drude-Condon model for Maxwell’s equations in isotropic optically active media. d, The Goos-Hänchen shift LGH of the evanescent wave.
and , are shown for evanescent-wave measurements of maltodextrin, glycerol (a non-chiral reference sample with zero optical rotation), and fructose solutions, all with refractive index n=1.442. The solutions are changed with a flow cell every 10 minutes. b, Subtractions of the polarization frequencies isolate the optical rotation of the samples in the evanescent wave, out of larger achiral backgrounds. c, Measurements for solutions with n=1.417-1.442. Error bars are 2σ confidence intervals. The theoretical curves are generated using the Drude-Condon model for Maxwell’s equations in isotropic optically active media. d, The Goos-Hänchen shift LGH of the evanescent wave.