Pauli Shielding and Breakdown of Spin Statistics
A new screening effect, due to the Pauli Exclusion Principle, termed Pauli shielding, has been discovered in fast ion-atom collision studies. Measurements were performed at the 5.5 MV Tandem accelerator of the Institute of Nuclear and Particle Physics at the NCSR Demokritos by the experimental atomic physics group of Prof. Theo J.M. Zouros with PhD students Ioannis Madesis and Angelos Laoutaris of the University of Crete in collaboration with Prof. Manolis P. Benis of the University of Ioannina. Calculations were carried out by the theory group of Prof. Alain Dubois with PhD student Jun Wen Gao of the Sorbonne University, Paris. This study showed that Pauli shielding plays a key role in the fundamental process of single electron capture (SEC), resulting in the breakdown of the spin statistics rule for populating the states involved. The process of SEC and spin statistics play an important role in the understanding and modeling of astrophysical and laboratory plasmas, as well as in biological effects and hadron therapy.
Using energetic two-electron carbon ion beams in the 1s2s 3S state in collisions with He gas targets, the SEC process involving the transfer of a target electron to the 2p orbital, primarily populates the 1s2s2p configuration resulting in the 1s2s2p 4P, 2P- and 2P+ states:
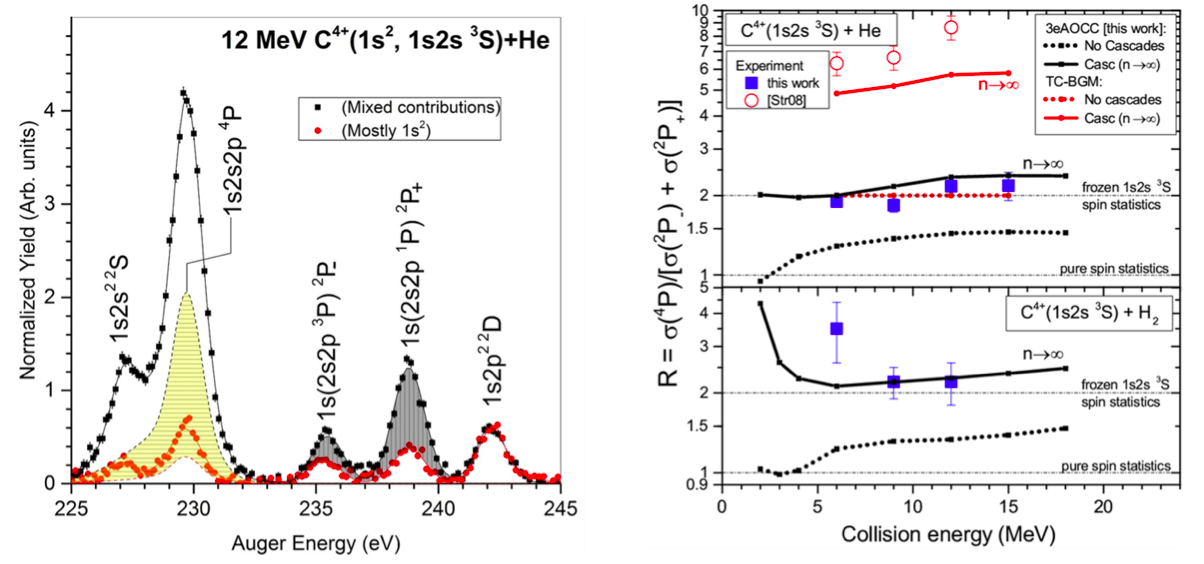
Groundbreaking, ab initio dynamical calculations involving three active electrons within a full configuration interaction approach were also performed for the first time for such a system. The calculated ratio R, after including cascade contributions from higher lying energy levels that primarily feed the 1s2s2p 4P state, was found to be in very good agreement with our measurements.
The important new understanding is that even for the short duration (≈ 3-25 ×10-18 s) of the collision, SEC dynamics are not properly described, neither by pure spin statistics nor by the frozen core approximations that use one active electron, as assumed so far. Novel strong electron correlation effects between the three active electrons, seem to play a vital role. Indeed, it was clearly shown that the population of the 1s2s2p 2P- state is strongly suppressed by Pauli shielding, and can only be populated via much weaker spin exchange interactions.
Research Article: “Pauli Shielding and Breakdown of Spin Statistics in Multielectron, Multi-Open-Shell Dynamical Atomic Systems” by I. Madesis, A. Laoutaris, T.J.M. Zouros, E.P. Benis, J.W. Gao, and A. Dubois, Phys. Rev. Lett. 124, 113401 (2020).




